数据压缩
编码
信源编码:关于随机变量
编码期望长度设随机变量
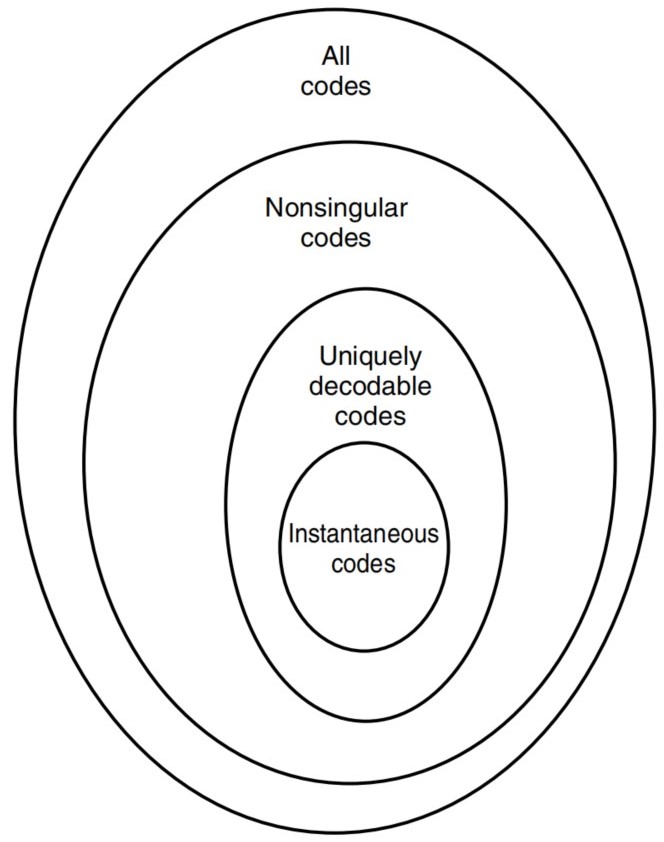
非奇异码:若编码将
则称这个编码是非奇异的
扩展编码:编码
其中
唯一可译码:若一个编码的扩展编码是非奇异的,则称该编码是唯一可译的
前缀码:若码中无任何码字是其他码字的前缀,则称该编码是前缀码或即时码
Kraft 不等式
Kraft 不等式:对于
反之,若给定满足以上不等式的一组码字长度,则存在一个相应的前缀码,其码字长度为给定的长度
证明:
考虑每一节点均含
个子节点的 叉树,假定数值代表码字的字符,每个码字均由树的 一片叶子表示,因此,始于根节点的路径可描绘出码字中的所有字符,码字的前缀条件表面树中无一码字是其他任一码字的祖先,因而,在这样的编码树中,每一码字都去除了它的可能称为码字的所有后代 令
为码字集中最长码字长度,考虑在树中 层的所有节点,可知其中有些是码字,有些是码字的后代,而另外的节点既不是码字,也不是码字的后代,在树中 层的码字拥有 层中 个后代,所有这样的后代集不相交,而且,这些集合中的总节点数必定小于或等于 ,因而,对所有的码字求和,则可得 即
反之,若给定任意一组满足Kraft不等式的码字长度
,总可以构造出满足条件的编码树,将第一个深度为 的节点标为1,同时除去树中属于它的所有后代,然后再剩余的节点中找出第一个深度为 的节点,将其标为码字2,同时除去树中所有属于它的所有后代,以此类推,即可构造出一个码字长度为 的前缀码
无限前缀码Kraft不等式:对任意构成前缀码的可数无限码字集,码字长度满足Kraft不等式
反之,若给定任意满足Kraft不等式的
最优码
定理:随机变量
当且仅当
证明:将期望长度与熵的差写成如下形式:
设
因此,
D进制:若对于某个
最优码长的界
定理:设
证明:设
从而有
但由于
定理:每字符最小期望码字长度满足
偏码定理:码字长度分配
证明:期望码长为
类似的,可以得到下界
唯一可译码Kraft不等式:任一唯一可译的
反之,若给定满足上述不等式的一组码字长度,则可以构造出具有同样码字长度的唯一可译码
赫夫曼码
赫夫曼码:

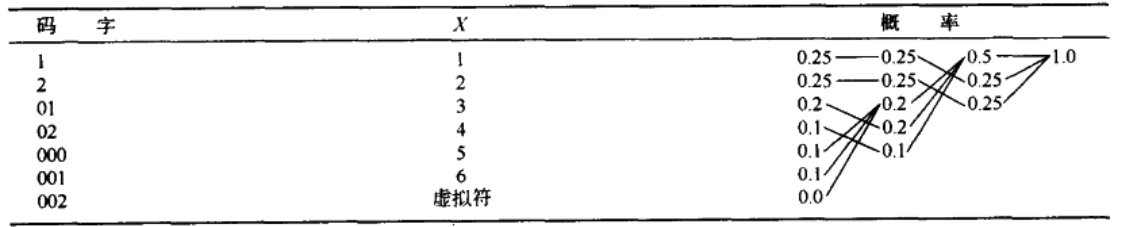
典则码:对于任何概率分布,存在一个最优前缀码满足以下性质
- 长度序列与按概率分布列排列的次序相反
- 两个最长的码字有着相同的长度
- 两个最长的码字只在最后一位不同,并对应于两个最不可能的符号
赫夫曼码最优性:赫夫曼码是最优的

