数理方程-热方程

热方程

基本解

基本解推导

计算热方程基本解 对方程进行傅里叶变换，可以得到关于的常微分方程问题 易得其解为

对它作傅里叶逆变换

作傅里叶变换：从磨光出发，

因此，的傅里叶变换为

热方程基本解：函数

称为热方程的基本解

基本解的积分：，则

证明：

---

初值问题

齐次初值问题

现在使用基本解来解决齐次初值问题

类似于基本解的推导，对方程和初值进行傅里叶变换

易得解为，对它作傅里叶逆变换，可得

非齐次初值问题

现在我们来讨论非齐次初值问题

法一：从基本解入手，对于无初值条件 存在弱解，为了类似的结果，构造辅助函数 此时，，且满足 此时，由基本解的性质可得 因此，原方程的解，只需验证初值条件即可

---

法二：从叠加原理、傅里叶变换、齐次化原理入手

• 叠加原理，可将原非齐次方程化为

  此时，方程的解，分别满足上述两个方程

• 由傅里叶变换可解得

• 再由齐次化原理来求解

• 代回原式，得到

---

齐次化原理

齐次化原理：若满足

令，则为柯西问题

的解

---

初边值问题

在这一节，我们考虑求解初边值问题

分离变量法

我们将利用分离变量法来求解此问题，不妨假设

否则作函数替换 则可得到一个关于的齐次边值问题

下面分别讨论初边值问题中非齐次项恒为零和不恒为零的情况

• 考虑分离变量形式的非零解 将它代入齐次方程得到 即 在上式中，左端是的函数，右端是的函数，因而只能是常数，记为，从而 将代入齐次边值条件，从而有 于是得到 此方程问题的所有非平凡特征值为 与特征值对应的解为 而与对应的为 从形式上看，每一个都满足方程和边值条件，但一般来讲他们都不满足初始条件，为求一个既满足方程和边值条件，又满足初始条件的解，将叠加，形式上， 满足方程，为使满足初始条件，我们需要 由于的完备性，可以得到 于是初边值问题的形式解为

• 此时仍可以利用分离变量法来求解，具体来说，把解，非齐次项和初值都按特征函数系展开，即 由特征函数系的正交性和完备性得到

  为求出未知函数，把上述表达式代入初边值条件中，由完备性，从而得到满足一下常微分方程的初值问题 求解此问题得到 代回的表达式，得到

---

极值原理

定义：设是中的有界开集，固定时间

• 定义抛物线圆柱体

• 定义抛物线边界

---

---

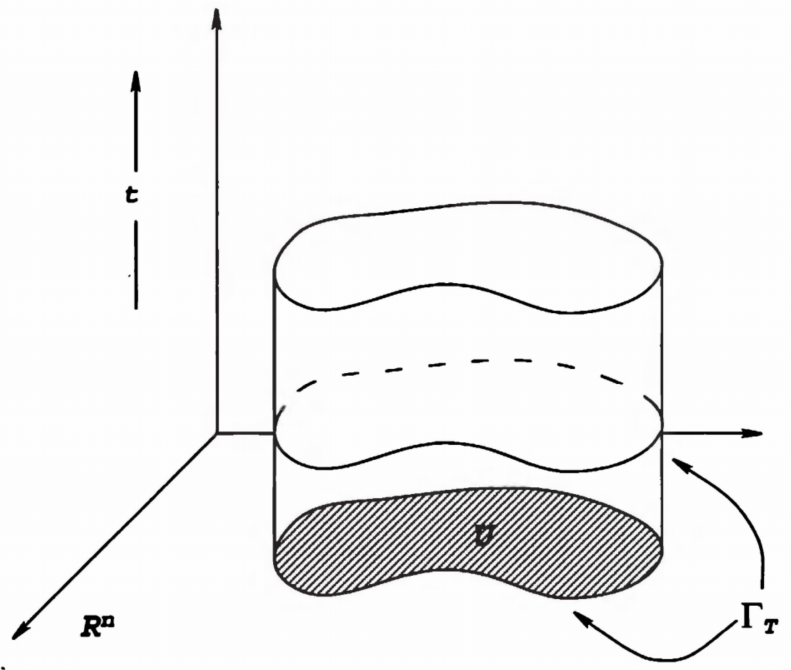
强极值原理：设是热方程的解，则

• 若是连通的且存在使得

  则

证明：由于，因此不等式成立

只需要证明 为此构造辅助函数 此时有 下面说明，在上的最大值不能在内达到，否则，存在一点使得 由微积分的定理可知 且 因此 矛盾！从而不可能在内达到的最大值，因此 于是 令，则得所需证明的不等式

---

推论：设是热方程的解，则在上的最小值必在抛物边界上达到

---

定理：设，则存在至多一个解关于初边值问题

证明：若是方程的两个解，令，则可知满足

由极值原理知，

---

初边值问题的唯一性和稳定性

定理：热传导方程

在上解唯一，且连续依赖于上的条件

证明：

• 唯一性

  设为热方程初边值问题的两解，令，则满足齐次方程零初值零边值，由极值原理，知，于是

• 稳定性

  若初值问题在上满足

  令为某热方程初边值问题的解，且在上

  由极值原理，知，稳定性成立

---

柯西问题的稳定性和唯一性

定理：热传导方程

在有界函数类中解唯一，且连续依赖于初值条件

证明：

• 唯一性

  设两个有界解，令，则有

  对，考虑区域

  构造

  在上连续

  • 内部：在内部满足齐次方程

  • 底边：

  • 侧边：

  于是有

  由极值原理，知

  即

  同理可证

  取，有

  令，有

  由的任意性，知

• 稳定性

  要证时，有，令

  同理可证，任取有

  令，有

  由的任意性，知

---