熵
熵
概率空间:设是一个样本空间,是上的域,P是上的概率测度,则称为概率空间
熵:设为随机变量,称是随机变量X的熵,即为X的不确定度,若X的概率分布为P,也可记作
- 是上的对称连续泛函
- 设n是一个大于2的正整数,定义 关于n不减
Grouping property:设,记第i个组为 则有
定理:设m和n是正整数,则满足
证明:应用Grouping Property 可以得到
推论:
定理:设n是正整数,则有
证明:设,则,s.t. 故可知 令N为任意正整数,则有 由于 从而有 由于N的任意性,知
熵:设 称是随机变量X在概率分布P上的熵
自信息:设,称X的自信息为
联合熵、条件熵
联合熵:称为联合熵,若一组离散随机变量
联合自信息: 若,则定义的联合自信息为
类似于单元随机变量,有 - 联合熵可以写成 - 联合熵可以写成
条件熵:若,则条件熵定义为
定理:
证明:
相对熵、互信息
相对熵:设是概率密度函数,称与的相对熵(Kullback-Leibler距离)为
Fundamental Inf Inequality:,当且仅当时等号成立
证明:
条件相对熵:设是联合概率分布,则条件相对熵为
互信息:设和是两个随机变量,同分布于联合概率,其边际分布为,则互信息是联合概率分布与边际分布之积的相对熵
我们可以重写互信息的定义为
因此,互信息是的不确定度在已知的信息下的减少量
由此,我们有 特别地,我们指出
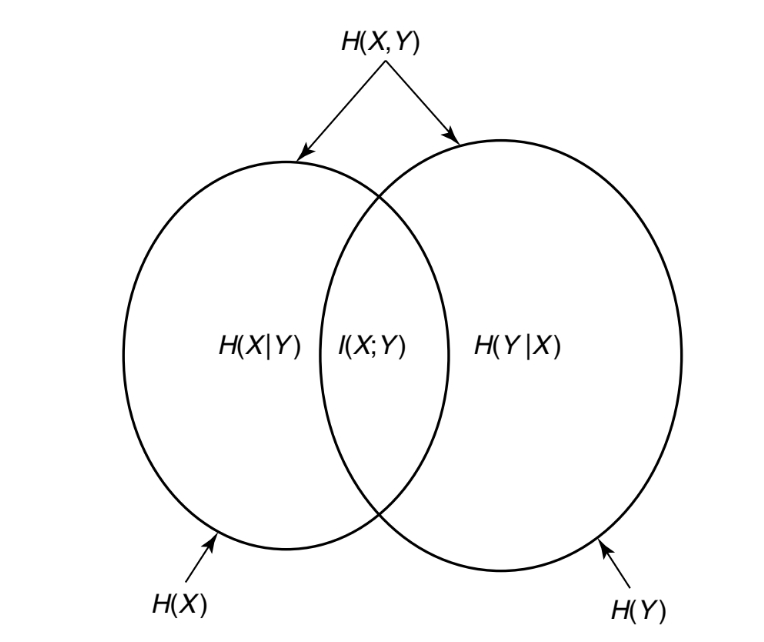
互信息与熵:
条件互信息:对于随机变量,条件互信息定义为
定理:
链式法则
熵链式法则:
法一: 重复利用二元随机变量的链式法则,有
法二:由于 故
条件熵链式法则:
互信息链式法则:
证明:
相对熵链式法则:
证明:
琴生不等式及其应用
凸函数:称是在上是凸函数,若满足,有 称是严格凸函数,当且仅当时,等号成立
琴生不等式:若是凸函数,是随机变量,则有
信息不等式:设是概率密度函数,则有 等号成立当且仅当
证明:设,则
互信息的非负性:对于任意两个随机变量,有 等号成立当且仅当独立
证明:
等号成立当且仅当,即独立
定理:,等号成立当且仅当
定理:,等号成立当且仅当在下条件独立
最大熵分布:,等号成立当且仅当X在上服从均匀分布
证明:设为上的均匀分布概率函数,为的概率密度函数,则
定理:,等号成立当且仅当独立
直观上,这个定理表明知道另一个随机变量能够降低的不确定度,同时也只能降低的不确定度,值得一提,这仅在平均时成立,特别地,可能大于或小于或等于,但一定有
定理:,等号成立当且仅当独立
证明:由熵链式法则
Log Sum 不等式及其应用
对数和不等式:对于非负数,有
当且仅当等号成立
证明:不失去一般性,可设,设,可知是严格凸函数,由Jensen不等式,有
令
于是得到 即
相对熵的凸性:设是两组概率密度函数对,则有
证明:
对所有的求和即可
熵的凹性:是关于的凹函数
证明:
其中是上的均匀概率分布,由的凸性,可得是凹函数
定理:设,互信息在固定是关于的凹函数,在固定是关于的凸函数
证明:
由于 若固定,则是的线性函数
由于是关于的凹函数,故也是关于的凹函数
由于是的线性函数,不影响凹凸性,从而是的凹函数
数据处理不等式
马尔科夫链:称随机变量构成马尔科夫链,若满足的条件分布只依赖于,与条件独立,即
数据处理不等式:若,则有
证明:由链式法则,有 由于条件独立,从而有,由于,则
推论:令,则有
推论:若,则有
证明:
由于,故
Fano 不等式
Fano 不等式:对于任意估计使得,且,则有
证明:定义错误随机变量 由链式法则 由于条件减少熵,故,同时由于是的函数,则条件熵,且有 从而得到 由于是马尔科夫链,由数据处理不等式,有 因此
推论:对于任意随机变量,令,则有
推论: 令,则
定理:设独立同分布,熵为,则有 等号成立当且仅当满足均匀分布
证明:设,由琴生不等式,得 即
推论: 设独立,,则有
证明:


