数值分析-插值法
插值问题
插值法概述
插值法:设函数在区间上有定义,且已知在点上的值,若存在一简单函数,使 成立,就称为的插值函数,点称为插值节点,包含插值节点的区间称为插值区间
多项式插值
多项式插值存在性唯一性定理:设在区间上给定n+1个点上的函数值,存在唯一次数不超过n的多项式,使
证明:由此可得关于系数的n+1元线性方程组
此方程组的系数矩阵为 由于互异,故 因此,方程组的解存在且唯一
拉格朗日插值
拉格朗日插值多项式
插值基函数:若n次多项式在n+1个节点上满足条件
就称这n+1个n次多项式为节点上的n次插值基函数
拉格朗日插值多项式:形如 的插值多项式称为拉格朗日插值多项式
插值余项与误差估计
定理:设在上连续,在内存在,节点,是满足条件的插值多项式,则对任何,插值余项 这里且依赖于x
证明:容易得到 为了求出,构造辅助函数 可得在区间上有共个零点,由罗尔定理,可知在区间上至少有个零点,以此类推,最后知在区间上存在一点,使得,即
牛顿插值
差商
差商: - 称为函数关于的一阶差商 - 称为的二阶差商 - 一般地,称 为的k阶差商
- 差商与节点的排序无关,称为差商的对称性,即
- n阶差商与导数的关系为
牛顿插值多项式
牛顿插值多项式:形如 的插值多项式称为牛顿插值多项式
牛顿插值余项
定理:牛顿插值多项式余项满足
埃尔米特插值
插值多项式要求在插值节点上函数值相等,但有的实际问题还要求在节点上导数值相等,甚至高阶导数值也相等,将满足这种要求的插值多项式称为埃尔米特插值多项式
两点三次埃尔米特插值
两点三次埃尔米特插值:插值节点取为及,插值多项式为,满足条件
解:采用基函数方法,令 其中是关于节点以及的三次埃尔米特插值基函数,它们应分别满足条件
于是求得 同理可求得
插值余项与误差估计
两点三次埃尔米特插值余项:若在存在,则对,两点三次Hermite插值的误差为
其中,且依赖于
分段低次插值
高次插值的病态性质
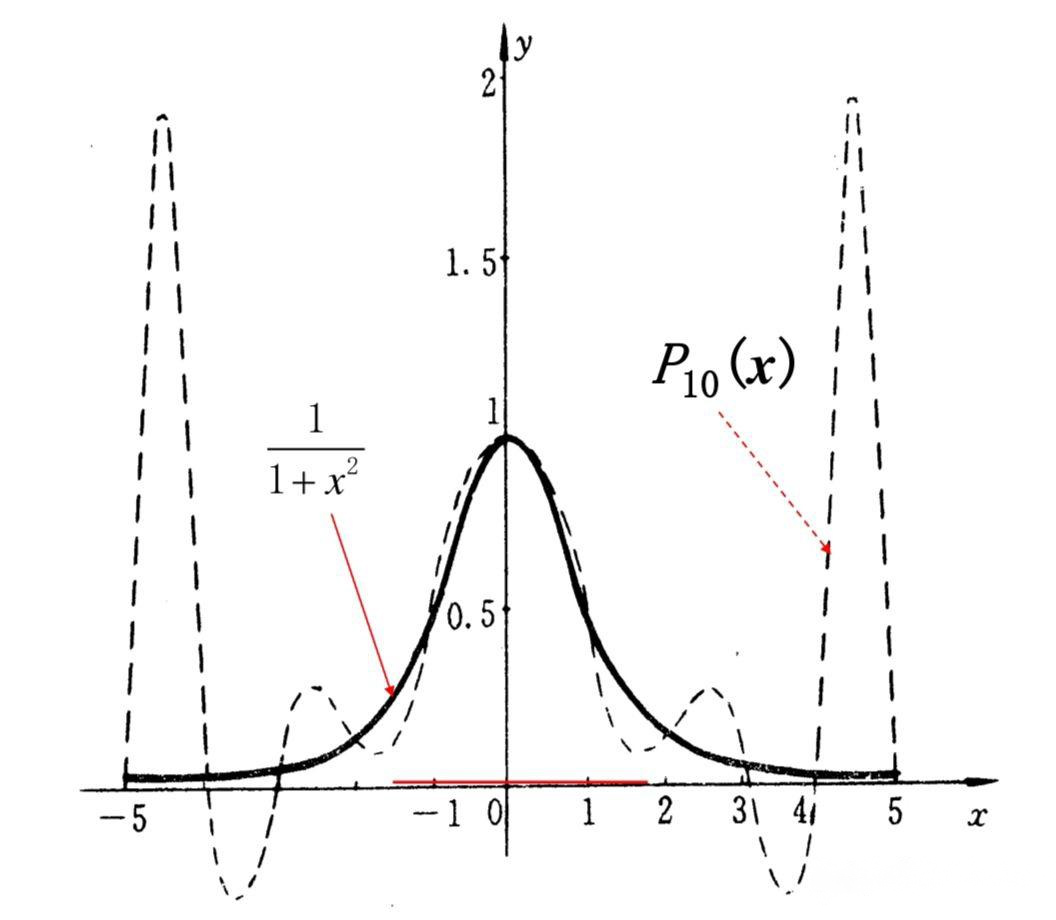
上面我们根据上给出的节点插值做插值多项式近似,一般总认为的次数n越高逼近的精度越好,但实际上并非如此。
这是因为对任意的插值节点,当时,不一定收敛于,即龙格现象
分段线性插值
分段线性插值函数:设已知节点
上的函数值 ,记,折线函数满足:
则称为分段线性插值函数
定理:若函数,则在上一致收敛到
证明:由定义可知,分段线性插值的误差估计可以用插值余项得到
其中,由此知
分段三次埃尔米特插值函数
分段线性插值函数的导数是间断的,若在节点上除已知函数值外还给出导数值,这样就可构造一个导数连续的分段插值函数
分段三次埃尔米特插值函数:满足条件
称为分段三次埃尔米特插值函数
误差估计:设,为在节点上的分段三次埃尔米特插值多项式,则有
其中
三次样条插值
三次样条插值函数:设函数,且在每个小区间上是三次多项式,若在节点上给定函数值,并成立
则称为三次样条插值函数
从定义知要求出,在每个小区间上要确定4个待定系数,而共有n个小区间,故应确定4n个参数。根据在上二阶导数连续,在节点处应该满足连续性条件
这里共有3n-3个条件,再加上满足插值条件,共有4n-2个条件,因此还需要加上2个条件才能确定。通常,可在区间的端点上各加一个条件(称为边界条件),可根据实际问题的要求给定。常见的有以下3种:
定理:型三次样条插值问题的解存在且唯一
证明:记,将其设为待定参数,由于在上为三次多项式,故在上为线性函数,于是可得的分段表达式 将上式积分两次,并利用来确定积分常数,可得
要证唯一存在,只需证明可被唯一确定
对于上述满足其自身和二阶导函数在整个区间上连续,由连接条件,还要求一阶导数在整个区间上连续,即
我们有
于是,单元右端点的左极限和左端点的右极限分别为
从而有
若记 则上式可化为 此外,在端点和处应分别右连续和左连续,利用附加边界条件,可得
化简得到 综合所有条件,可以得到一个关于待定参数的阶线性代数方程组,其矩阵形式为
显然方程组的系数矩阵是严格对角占优的,因此非奇异,于是可以唯一的解出,从而得到型三次样条插值问题的解存在且唯一
三次样条插值函数的基本性质
定理:若是型三次样条插值函数,则对,有
证明:令,则,且满足 对,有
最佳逼近定理:若是型三次样条插值函数,则对,有
证明:利用引理及Cauchy不等式,有 从而


